Chapitre 8 - Probabilités
- Construire un arbre correspondant à une situation donnée.
- Construire un tableau correspondant à une situation donnée.
- Déterminer l’ensemble des issues possibles.
- Déterminer l’ensemble des issues correspondant à un événement.
- Calculer la probabilité d’un événement dans une situation d’équiprobabilité.
- Connaitre et utiliser les notations de réunion et d'intersection.
- Décrire et déterminer la probabilité de la réunion de deux évènements.
- Décrire et déterminer la probabilité d'un évènement contraire.
IVocabulaire : Evenements aléatoires, issues
 Toutes les issues sont dans l'ensemble \(\Omega\) et aucune autre éventualité.
Toutes les issues sont dans l'ensemble \(\Omega\) et aucune autre éventualité.

- L'évènement "faire un nombre pair" n'a que 3 issues possibles et correspond au sous-ensemble \(\{2,4,6\}\)
- L'évènement "faire plus que 4" n'a que 2 issues possibles et correspond au sous-ensemble \(\{5,6\}\)
- Un évènement A est une partie ou un sous-ensemble de l'ensemble des issues possibles \(\Omega\)
- Un évènement qui ne contient qu'une issue est appelé un évènement élémentaire
- "faire tout sauf 1 et 6"
- "faire entre 1 et 5"
- "faire 2 ou 3 ou 4 ou 5"
- etc.
- \(\Omega\) est un évènement il correspond à "tout peut arriver"
- \(\emptyset\) est l'évènement sans aucune issue, et donc impossible
IICalcul de probabilités
- \(R\) : "tirer un boule rouge"
- \(V\) : "tirer un boule verte"
- \(B\) : "tirer un boule bleue"
- La probabilité de l 'évènement certain \(\Omega\) vaut 1 : \(p (\Omega) = 1\)
- La probabilité de l 'évènement impossible \(\emptyset\) vaut 0 : \(p (\emptyset) = 0\)
On considère un évènement \(E\) dans une expérience aléatoire donnée.
Si l'on répète \(N\) fois l'expérience aléatoire, l'évènement \(E\) se produira "environ" \(p (E) \times N\) fois.
L'approximation sera d'autant plus précise si le nombre de répétitions \(N\) est grand
En reprenant l'exemple de l'expérience "jouer à pile ou face". La probabilité que l'évènement "pile" se produise est \(\frac{1}{2}\).
Si l'on joue \(N=1000\) fois, on obtiendra environ \(p (pile) \times N = \frac{1}{2}\times 1000 = 500 fois pile\)
En reprenant l'exemple de l'expérience des boules de couleur (1 rouge, 2 vertes, 3 bleues). La probabilité que l'évènement "tirer une boule verte" se produise est \(\frac{1}{3}\).
Si l'on joue \(N=1200\) fois, on obtiendra environ \(p (V) \times N = \frac{1}{3}\times 1200 = 400 fois une boule verte\)
- "tirer un dé équilibré" est une situation d'équiprobabilité
- "tirer un dé pipé" n'est pas une situation d'équiprobabilité
Tirer une carte dans un paquet de 32 cartes est une situation d'équiprobabilité. On note \(A\) l'évènement "tirer un as"

L'univers \Omega comprend 32 issues et il y a 4 as : \(A = \{A♥,A♦,A♣,A♠\}\)
Donc \(p (A) = \frac{4}{32} = \frac{1}{8}\). Il y a une chance sur 8 de tirer un as.
IIIRéunion, intersection et évènement contraire
1Généralités
- L'événement \(A \cup B\) est constitué des issues qui appartiennent soit à A, soit à B, soit aux deux ensembles.
- L'événement \(A \cap B\) est constitué des issues qui appartiennent à la fois à A et à B.
- L'évènement \(\bar{A}\) est constitué des issues qui ne sont pas des issues de A
- \(A \cup B\) se lit « \(A\) union \(B\) » ou « \(A\) ou \(B\) »
- \(A \cap B\) se lit « \(A\) inter \(B\) » ou « \(A\) et \(B\) »
- \(\bar{A}\) se lit « \(A\) barre » ou « le contraire de \(A\) »
- \(A\) "obtenir un nombre pair" : \(A = \{2,4,6\}\)
- \(B\) "obtenir moins que 4" \(B = \{1,2,3\}\)
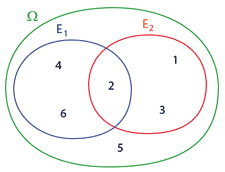 Il est possible d'obtenir un des deux évènements, les deux à la fois ou aucun des deux :
Il est possible d'obtenir un des deux évènements, les deux à la fois ou aucun des deux : - \(A\cup B\) "obtenir un nombre pair ou un nombre plus petit que 4" : $$A\cup B = \{1,2,3,4,6\}$$
- \(A\cap B\) "obtenir à la fois un nombre pair et plus petit que 4" : $$A\cap B = \{2\}$$
- \(\bar{A}\) "obtenir un nombre impair" : $$\bar{A} = \{1,3,5\}$$
2Calculs
Les évènement "faire un nombre pair" et "faire un nombre impair" sont incompatibles.
L'intersection entre \(\{2,4,6\}\) et \(\{1,3,5\}\) est vide : \(A\cap B = \emptyset\).On reprend l'exemple de la partie précédente III-1 où \(A\) est "obtenir un nombre pair" et \(B\) est "faire moins que 4".
On a \(p (A) = \frac{1}{2}\), \(p (B) = \frac{1}{2}\) et comme \(A \cap B = \{2\}\) contient un seul élément \(p (A \cap B) = \frac{1}{6}\).
Si on applique la formule : $$p (A \cup B) = p (A) + p (B) - p (A \cap B) = \frac{3}{6} + \frac{3}{6} - \frac{1}{6} = \frac{5}{6}$$
On vérifie facilement que c'est vrai car on a vu que \(A \cup B\) contenait 5 issues.- \(\bar{A}\) "otenir un nombre impair" a pour probabilité : \(p (\bar{A}) = 1 - p (A) = 1 - \frac{1}{2} = \frac{1}{2}\)
- \(\bar{B}\) "otenir un nombre plus grand que 3" a pour probabilité : \(p (\bar{B}) = 1 - p (B) = 1 - \frac{1}{2} = \frac{1}{2}\)
IVArbres et tableaux
1Tableaux
2Arbre de Probabilités
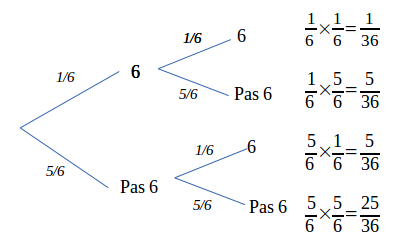 Les probabilités des deux jets se multiplient ;
Les probabilités des deux jets se multiplient ;
- La probabilité de faire 6 puis encore 6, noté (6;6) vaut donc \(\frac{1}{36}\)
- L'évènement « Faire une seule fois 6 » est composé des deux évènements indépendants (6 ; pas 6) et (pas 6 ; 6) qui s'ajoutent : \(\frac{5}{36} + \frac{5}{36} = \frac{10}{36}\)